斐波那契数列 Fibonacci
递推公式
设 $F_n$ 为数列的第 $n$ 项,那么有递推公式 $F_n = F_{n-1} + F_{n-2}$ 。
通项公式
\[F_n = \frac{1}{\sqrt{5}}[(\frac{1+\sqrt{5}}{2})^n-(\frac{1-\sqrt{5}}{2})^n]\]此时 $ F_1 = 1, F_2 = 1 $
性质
平方与前后项
从第二项开始,每个奇数项的平方都比前后两项之积多$1$,每个偶数项的平方都比前后两项之积少$1$。
奇数项求和
\[F_1 + F_3 + F_5 + F_7 + \cdots + F_{2n-1} = F_{2n} - F_2 + F_1\]当$ F_1 = F_2 = 1 $时,有
\[F_1 + F_3 + F_5 + F_7 + \cdots + F_{2n-1} = F_{2n}\]偶数项求和
\[F_2 + F_4 + F_6 + F_8 + \cdots + F_{2n} = F_{2n+1} - F_1\]平方求和
\[F_1^2 + F_2^2 + F_3^2 + F_4^2 + \cdots + F_n^2 = F_nF_{n+1}\]隔项之和
\[F_{2n-2m-2} = F_{2n} + F_{2n+2} = F_{2m+2} + F_{4n-2m}\]此时$ n > m \geq -1 $,且$ n \geq 1 $
隔项之积
\[F_{n-1}F_{n+1} = (-1)^n + F_n^2\]两倍项关系
\[F_{2n} = F_{n}(F_{n-1}+F_{n+1})\]其他公式
\[F_1 + 2F_2 + 3F_3 + 4F_4 + \cdots + nF_n = nF_{n+2} - F_{n+3} + 2\]Zeckendorf定理
任何正整数都可以表示成若干个不连续的斐波那契数(不包括第一个斐波那契数)之和。这种和式称为齐肯多夫表述法。而对于任何正整数,其齐肯多夫表述法都可以由贪心算法(即每次选出最大可能的斐波那契数)得到。
帕斯卡/杨辉三角形
递推公式
设 $ T_{(n,m)} $ 为帕斯卡三角形第 $n$ 行第 $m$ 列的数,则有:
\[T_{(n,m)} = T_{(n-1,m-1)} + T_{(n-1,m)}\]性质
-
帕斯卡三角形以正整数构成,数字左右对称,每行由$1$开始逐渐变大,然后变小,回到$1$。
-
帕斯卡三角形的第$n$行有$n$个数字。
-
第$n$行的第$m$个数字$T_{(n,m)}$即为组合数$C_{n-1}^{m-1}$的值。
-
第$n$行的$n$个数字正好对应于二项式$(a+b)^{n-1}$展开后的系数。
-
第$n$行的数字之和为$2^{n-1}$。
卡特兰数 Catalan
递推公式
设 $ H_n $ 为第 $n$ 项卡特兰数,且 $H_0 = 1, H_1 = 1$,则有:
\[H_n = H_0H_{n-1} + H_1H_{n-2} + H_2H_{n-3} + \cdots + H_{n-1}H_0 \ (n \geq 2)\]或者有:
\[H_n = H_{n-1} \frac{4n-2}{n+1}\]通项公式
\[H_n = \frac{C_{2n}^{n}}{n+1}\]或者:
\[H_n = C_{2n}^{n}-C_{2n}^{n-1}\]其中,$n$均大于等于$0$。
应用
矩阵连乘/括号正确匹配数
-
有式子$ A_1 \times A_2 \times A_3 \times \cdots \times A_n $,不改变其中乘数的顺序和最终的结果,仅根据乘法结合律添加括号,共有 $H_n$ 种方案。
-
用$n$对括号,合法的匹配方案数为 $H_n$ 种。
出栈次序
已知一个没有深度限制的栈的入栈序列为 $A_1, A_2, A_3, \cdots, A_n$,那么合法的出栈序列共有 $H_n$ 种。
凸多边形三角划分
在一个凸$n$边形中,用若干条互不相交的对角线划分成若干个三角形的划分方案数共有 $H_n$ 种。
给定节点组成二叉树
用节点数$n$能够成 $H_n$ 种不同的二叉树。
斯特林数 Stirling
第一类斯特林数
递推公式
\[s(n,m) = s(n-1,m-1) + (n-1) \times s(n-1,m)\]性质
-
$ s(0,0) = 1 $
-
$ s(n,0) = 0 $
-
$ s(n,1) = (n-1)! $
-
$ s(n,n-1) = C_n^2 $
-
$ s(n,n) = 1 $
应用
将 $n$ 个不同元素构成 $m$ 个圆排列的方案数为 $S(n,m)$
第二类斯特林数
递推公式
\[S(n,m) = S(n-1,m-1) + m \times S(n-1,m)\]性质
-
$ S(n,0) = 0 $
-
$ S(n,1) = 1 $
-
$ S(n,n-1) = C_n^2 $
-
$ S(n,n) = 1 $
应用
将 $n$ 个不同元素拆分成 $m$ 个集合的方案数为 $S(n,m)$
两类斯特林数之间的关系
\[\displaystyle\Sigma_{k=0}^n S(n,k)s(k,m) = \Sigma_{k=0}^n s(n,k)S(k,m)\]其中 $s$ 表示第一类斯特林数, $S$ 表示第二类斯特林数。
求和公式
等差数列求和
\[Sum = \frac{n(A_1+A_n)}{2}\]其中,$A_1$ 为首项,$A_n$ 为末项,$n$ 为项数。
等比数列求和
\[Sum = A_1 \frac{1-q^n}{1-q} = \frac{A_1-A_nq}{1-q}\]其中,$A_1$ 为首项, $A_n$ 为末项,$n$ 为项数,$q$ 为公比,且 $q \not= 1$ 。
等差数列平方和
\[Sum = \frac{n(A_1+A_n)^2}{4} + \frac{nd^2(n^2-1)}{12}\]其中,$A_1$ 为首项,$A_n$ 为末项,$n$ 为项数,$d$ 为公差。
特殊数列求和
\[1 + 2 + 3 + \cdots + n = \frac{n(n+1)}{2}\] \[1^2 + 2^2 + 3^3 + \cdots + n^2 = \frac{n(n+1)(2n+1)}{6}\] \[1^3 + 2^3 + 3^3 + \cdots + n^3 = \frac{n^2(n+1)^2}{4}\] \[1 + 3 + 5 + 7 + \cdots + (2n-1) = n^2\]矩阵树定理
拉普拉斯矩阵(基尔霍夫矩阵)
其实就是图的出度矩阵-入度矩阵罢了
比如对于这个无向图
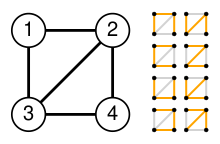
可以构造拉普拉斯矩阵 $Q$ :
\[Q= \left[ \begin{matrix} 2 & -1 & -1 & 0 \\ -1 & 3 & -1 & -1 \\ -1 & -1 & 3 & -1 \\ 0 & -1 & -1 & 2 \\ \end{matrix} \right]\]矩阵树定理
然后你只需要对构造出的拉普拉斯矩阵去掉任意一行任意一列再求行列式即可
比如用上面的例子,可以对下面这个矩阵 $Q’$ 求 $det$ (去除了第一行第一列)
\[Q'= \left[ \begin{matrix} 3 & -1 & -1 \\ -1 & 3 & -1 \\ -1 & -1 & 2 \\ \end{matrix} \right]\]得到的结果即为该无向图(可以有重边)的生成树个数
扩展
将矩阵树定理应用在有向图上,就可以计算树形图的个数
将有向图 $G$ 的拉普拉斯矩阵去掉第 $i$ 行和第 $i$ 列,求得的行列式值就是以 $i$ 为根的树形图的个数。
证明
改天等我看懂了再写吧233
欧拉回路
定义
无向图:
1) 设G是连通无向图,则称经过G的每条边一次并且仅一次的路径为欧拉通路;
2) 如果欧拉通路是回路(起点和终点是同一个顶点),则称此回路为欧拉回路(Euler circuit);
3) 具有欧拉回路的无向图G称为欧拉图(Euler graph)。
有向图:
1) 设D是有向图,D的基图连通,则称经过D的每条边一次并且仅一次的有向路径为有向欧拉通路;
2) 如果有向欧拉通路是有向回路,则称此有向回路为有向欧拉回路(directed Euler circuit);
3) 具有有向欧拉回路的有向图D称为有向欧拉图(directed Euler graph)。
判断存在性
假设图均连通
无向图欧拉路径 : 含有恰好两个或不含度为奇数的点
无向图欧拉回路 : 不含有度为奇数的点
有向图欧拉路径 : 有恰好一个顶点出度比入度大 $1$,另有恰好一个顶点入度比出度大 $1$,其余都是出度 $=$ 入度。
有向图欧拉回路 : 每个顶点的入度与出度相等
混合图欧拉回路 : 假设有一张图有向图 $G’$,在不论方向的情况下它与 $G$ 同构。并且 $G’$ 包含了 $G$ 的所有有向边。那么如果存在一个图 $G’$ 使得 $G’$ 存在欧拉回路,那么G就存在欧拉回路。 其思路就将混合图转换成有向图判断。实现的时候,我们使用网络流的模型。现任意构造一个 $G’$ 。用 $I_i$ 表示第 $i$ 个点的入度,$O_i$ 表示第 $i$ 个点的出度。如果存在一个点 $k$,$|O_k-I_k| \mod 2=1$,那么 $G$ 不存在欧拉回路。接下来则对于所有 $I_i>O_i$的点从源点连到i一条容量为 $\frac{I_i-O_i}{2}$ 的边,对于所有 $I_i<O_i$ 的点从 $i$ 连到汇点一条容量为 $\frac{Oi-Ii}{2}$ 的边。如果对于节点 $U$ 和 $V$ ,无向边 $(U,V) \in E$ ,那么 $U$ 和 $V$ 之间互相建立容量为 $1$ 的边。如果此网络的最大流等于 $\Sigma\frac{|I_i-O_i|}{2}$ ,那么就存在欧拉回路。
BEST 定理
BEST 定理用于有向图的欧拉回路计数
概述
\[Ans = H(G) \times \Sigma_{u \in V} (deg(u)-1)!\]$H(G)$ 即为图 $G$ 的根为 $1$ 的树形图个数, $deg(u)$ 为点 $u$ 的出度。
构造&证明
先贴一个有点假的讲解 : here
首先我们看一下如何构造回路。
由于是回路,所以为了避免重复,我们先规定回路从 $1$ 号点出发,并钦定一条起始边。
我们先找到一个以点 $1$ 为根的有向树,满足树上的每个点都可以通过树边连向 $1$ 号点。然后我们给每个点连出去的非树边钦定一个顺序。有了这些,我们就可以这样构造一条欧拉回路:
一开始在 $1$ 点。每次到一个点时(包括出发时),按照钦定的顺序,沿着第一条没有走过的非树边走出去。如果该点连出去的非树边都被走过了,那么就走树边。这样下去知道回到点 $1$ 并且无边可走就结束。
为什么最后一定会回到1号点?
因为所有点入度等于出度,有进必有出。
为什么这样走所有的边会被恰好走过一次?
首先显然所有的边会被走过最多一次。
那么为什么每条边至少走过一次?
观察两个性质:
-
如果一个点还没有走完非树边,那么他连出的树边也肯定没有走过。
-
如果一个点的连出树边没有走过,那么他连出的树边的对应点的树边肯定也没走过。因为入度等于出度,还有一个没进就不会出最后一个。
那我们假设有某条边没有走过,那么相应点的树边也没走过,那么树边连下去的点也都没走过,那么 $1$ 号点也肯定有至少一条入边没有走过,于是矛盾了,这个假设不成立。原命题成立。
那么求方案的话,我们只要求出图中所有根为 $1$ 的内向树的个数,在乘上每个点的非树边的个数的阶乘(钦定的顺序的方案数)即可。
哈密顿回路
定义
哈密顿图(哈密尔顿图)(Hamiltonian path)是一个无向图,由天文学家哈密顿提出,由指定的起点前往指定的终点,途中经过所有其他节点且只经过一次。在图论中是指含有哈密顿回路的图,闭合的哈密顿路径称作哈密顿回路(Hamiltonian cycle),含有图中所有顶点的路径称作哈密顿路径。
判断存在性
-
Dirac定理(充分条件) : 设一个无向图中有 $N$ 个顶点,若所有顶点的度数大于等于 $\lceil\frac{N}{2}\rceil$ ,则哈密顿回路一定存在.
-
基本的必要条件 : 设图 $G=<V, E>$ 是哈密顿图,则对于 $v$ 的任意一个非空子集 $S$ ,若以 $Num$ 表示 $S$ 中元素的数目, $G-S$ 表示 $G$ 中删除了 $S$ 中的点以及这些点所关联的边后得到的子图,则 $W(G-S)<=Num$ 成立.其中 $W(G-S)$ 是 $G-S$ 中联通分支数.
-
竞赛图(哈密顿通路) : $N \ (N \geq 2)$ 阶竞赛图一点存在哈密顿通路.


